Ur detta får vi sedan

vilket är tillåtligt, då  är en kvot mellan två längder och uppenbart är nollskild. Denna andragradsekvation har då två reella rötter, nämligen:
är en kvot mellan två längder och uppenbart är nollskild. Denna andragradsekvation har då två reella rötter, nämligen:
 är en kvot mellan två längder och uppenbart är nollskild. Denna andragradsekvation har då två reella rötter, nämligen:
är en kvot mellan två längder och uppenbart är nollskild. Denna andragradsekvation har då två reella rötter, nämligen: .
.
Decimal approximation av rötterna
Den andra lösningen är uppenbart felaktig, då  som en kvot mellan längder måste vara positiv. Inte desto mindre är den intressant, eftersom
som en kvot mellan längder måste vara positiv. Inte desto mindre är den intressant, eftersom 
 som en kvot mellan längder måste vara positiv. Inte desto mindre är den intressant, eftersom
som en kvot mellan längder måste vara positiv. Inte desto mindre är den intressant, eftersom 
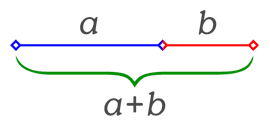
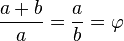
 erhålls
erhålls


Inga kommentarer:
Skicka en kommentar